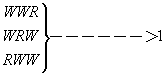
ｗｗｗ ─────＞０ ｆ（０）＝（０.７）３有一箱子裝有３個紅球與７個白球，今從此箱中以放回抽樣的方式抽出３個球，令Ｘ代表所抽出的紅球個數，試求Ｘ的機率分配：
解：基本上這是一個計算機率分配的問題，先找出此隨機試驗的樣本空間Ｓ，然後根據隨機變數Ｘ的定義最出其可能值Ｘ，最後再分別求出每一Ｘ值之機率，則為我們所要求的機率分配。茲以Ｒ代表紅球，Ｗ代表白球，則其樣本空間Ｓ，機變數Ｘ之可能值以及機率示如下：
樣本空間 隨機變數可能值Ｘ 機率分配
Ｓ 隨機變數可能值Ｘ ｆ（ｘ）
ｗｗｗ ─────＞０ ｆ（０）＝（０.７）３
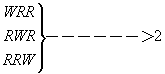
ＲＲＲ ─────＞３ ｆ（３）＝（０.３）３
若以公式表現ｆ（ｘ），則為：
※f(0)+f(1)+f(2)+f(3)=1
由於採放回抽樣，故為獨立的隨機試驗，且每次試驗（抽球）抽出紅球（定義為成功）的機率皆為０.３，而抽出白球（定義為失敗）對機率為０.7，因此符合二項實驗的特性，故ｆ（ｘ）為二項分配。
在二項分配的公式ｆ（ｘ）中，ｘ表示成功的次數（抽出紅球的個數），而成功機率ｐ＝０.３，因此為（０.３）ｘ；同理失敗次數（抽出的白球個數）為３－ｘ，故其機率為（０.３）３－ｘ。另外，ｆ（ｘ）的係數乃是由二項公式（ｂｉｎｏｍｉａｌ ｃｏｅｆｆｉｃｉｅｎｔ）。二項公式如下：
其中
乃組合符號，表示ｎ次試驗中，成功（ｙ）的次數有ｘ次，而失敗（ｚ）次數ｎ－ｘ次，則其可能情形共有C(n,x)
個，此即二項係數。就本例而言，ｎ＝３，故成功ｘ次，失敗（３－ｘ）次的可能情形有C(3,x)
個。